در صورتی که آماده هستید، به سؤالات زیر پاسخ دهید و بررسی کنید که چه نمرهای میگیرید.
در صورتی که نیاز به مطالعه این درس دارید، اینجا کلیک کنید.
دسته: اعداد گویا
کاربرگ ضرب اعداد گویا
در صورتی که آماده هستید، به سؤالات زیر پاسخ دهید و بررسی کنید که چه نمرهای میگیرید.
در صورتی که نیاز به مطالعه این درس دارید، اینجا کلیک کنید.
کاربرگ تفریق اعداد گویا
در صورتی که آماده هستید، به سؤالات زیر پاسخ دهید و بررسی کنید که چه نمرهای میگیرید.
در صورتی که نیاز به مطالعه این درس دارید، اینجا کلیک کنید.
کاربرگ جمع اعداد گویا
در صورتی که آماده هستید، به سؤالات زیر پاسخ دهید و بررسی کنید که چه نمرهای میگیرید.
در صورتی که نیاز به مطالعه این درس دارید، اینجا کلیک کنید.
خصوصیت 4
4- مقايسه اعداد گويا:
با من همراه بشويد تا ترفند سريعي براي مقايسه دو عدد گويا پيدا كنيم.
با توجه به قسمت قبل ميدانيم:

يعني هر رابطهاي بين اين دو عدد به دست آيد براي كسرهاي بالاي سر آنها هم صحيح است.
و اين همان ترفند جادويي ماست.
به اين عمل «طرفين- وسطين كردن» ميگويند كه البته اصطلاح صحيح آن «حاصلضرب طرفين برابر با حاصلضرب وسطين» است.
اصطلاحات طرفين و وسطين از قديم كه كسرها را به صورت تقسيمي مينوشتهاند، آمدهاند :
3÷5=9÷15
3 و 15 در طرفين و 9 و 5 در وسط قرار ميگيرند.
اما درباره اعداد منفي چطور؟
راه، فرقي نخواهد كرد اما يك نكته مهم وجود دارد. با هم ببينيم!
مثال: چه رابطهاي بين اين دو كسر است؟
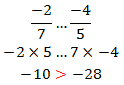
و اينجاست آن نكته مهم!
28- روي محور عقبتر از 10- قرار دارد پس نبايد گول ظاهر بزرگش را خورد.
پس
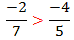
اما اگر بخواهيم تعداد بيش از دو كسر را با هم مقايسه كنيم:
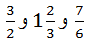
آيا اين روش باز هم سادهترين راه است؟
نگران نباشيد راههاي زيادي براي مقايسه اعداد گويا وجود دارد. حالا يكي از راههاي مفيدش را با هم پيدا ميكنيم.
بگذاريد از اينجا شروع كنيم:
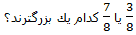
بياييد دوباره به يك پيتزا فكر كنيم. شما هم پيتزا را دوست داريد اينطور نيست؟
آن را به 8 قسمت برش ميزنيم يعني به اندازهي عدد مخرج كسر:

اگر خيلي گرسنه باشيد، 3 قطعه را ترجيح ميدهيد بخوريد؟ يا 7 قطعه را؟
البته 7 قطعه بهتره!
پس:
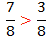
اوه! اين يعني از بين كسرهايي كه مخرجهاي يكساني دارند كسري بزرگتر است كه صورت بزرگتري دارد.
اما درباره كسرهايي با صورتهاي مساوي چه ميتوان گفت؟
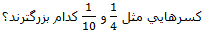
به اين پيتزاها نگاه كن باز هم اگر خيلي گرسنه باشي يك قطعه از كدام پيتزا را ترجيح ميدهي؟


از دو كسر كه صورتهاي برابر دارند كسري بزرگتر است كه مخرج كوچكتري داشته باشد. يعني تعداد تقسيمات آن كمتر باشد.
حالا برگرديم به سؤال اصلي خودمان.

بازی اول:
برای تمرین بیشتر، سعی کنید با پاسخ به سؤالاتی که در بالای بازی زیر مطرح میشود، در مسابقه طنابکشی برنده شوید:
بازی دوم:
با ترازویی که در بازی زیر وجود دارد، کسرهای بزرگتر و مساوی و کوچکتر را شناسایی کن:
http://pbskids.org/cyberchase/games/equivalentfractions/index.html
خصوصیت 3
3- اعداد مخلوط (Mixed Numbers)
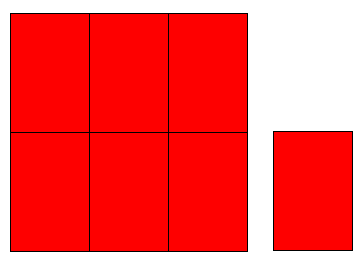
كسرهاي بزرگتر از واحد:
يا كسرهاي بزرگتر از 1، يعني كسرهايي كه صورت آنها از مخرج بزرگتر است.
مثل 7/6
اما بگذاريد ببينيم معني آن چيست؟ به اين شكل كه 7 قطعه به اندازه 1/6 را نشان ميدهد، نگاه كنيد.
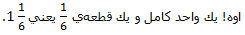

خصوصیت 2
2- داشتن بينهايت حالت نمايش مختلف:
مثال1:
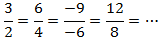
مثال2:
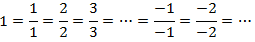
الف) ساخت اعداد گوياي مساوي:
مثال1: ميخواهيم 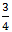 را به صورت كسري مساوي با آن بنويسيم كه مخرجش 16 باشد.
را به صورت كسري مساوي با آن بنويسيم كه مخرجش 16 باشد.
براي اين كار سه نكته را با هم يادآوري ميكنيم:
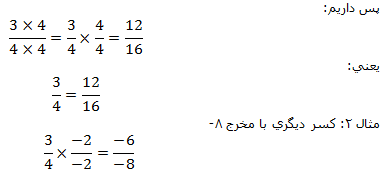
ب) تبديل كسر به سادهترين صورت ممكن:
ميخواهيم كسري مساوي با 100/200 بنویسیم كه از كوچكترين اعداد ممكن در آن استفاده شده باشد.
شايد سادهترين راه، تقسيم صورت و مخرج بر عدد 100 باشد. یعنی:
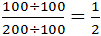
اما اين يكي چطور؟
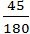
كمي سختتر است. نه؟
بياييد اين طور شروع كنيم:
هر دوي اعداد صورت و مخرج به چه عدد يكساني ميتوانند تقسيم شوند؟
بله به 3!

اما آيا راه بهتري وجود ندارد كه بتوانيم با يك بار تقسيم، سادهترين كسر را پيدا كنيم؟
بله، بهترين راه پيدا كردن ب. م. م يعني بزرگترين مقسوم عليه مشترك دو عدد 45 و 180 است. يعني عدد 45، كه براي پيدا كردن آن هم از روش نردباني و هم از روش نوشتن مقسوم عليههاي هر دو عدد و يافتن بزرگترين عامل مشترك، ميتوانيد استفاده كنيد.
بنابراين:
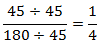
پس با تقسيم كردن صورت و مخرج يك كسر به ب. م. م آن دو، سادهترين كسر ممكن به دست خواهد آمد.
اگر نتوانستيد ب. م. م را بيابيد از همان روش اول استفاده كنيد.
بازی اول: برای درک بهتر، بازی زیر را انجام دهید:
روی Begin کلیک کنید و حدس بزنید جواب ساده شدهی کسر چه میشود:
بازی دوم: روی محوطه زیر کلیک راست کنید و Play را انتخاب کنید. سپس روی دکمه start کلیک کنید و هنگامی که بازی آغاز شد، با کلیدهای چپ و راست و Space (فاصله) بازی کنید و سفینههایی را منفجر کنید که با کسر روی اسلحه شما مساوی هستند. به طور مثال اگر روی سلاح نوشته شده است 4to6 (یعنی نسبت 4 به 6) باید سفینهای را منفجر کنید که کسر 2/3 (که مساوی با 4/6 است) روی آن نوشته شده است و یا کسر مساوی دیگری.
بازی سوم:
به صفحه زیر بروید و بازی را شروع کنید:
http://www.arcademicskillbuilders.com/games/ratio-stadium/ratio-stadium.html
یک موتور را انتخاب کنید. سرعت موتور شما در مسابقه، پاسخ به سؤالاتی است که در بالای بازی نمایش داده میشود. باید کسری که مساوی با کسر نمایش داده شده است را انتخاب کنید تا سرعتتان افزایش یابد.
میتوانید با دوستانتان مسابقه آنلاین برگزار کنید.
برای مشاهده ادامه مطلب، اینجا کلیک کنید…
ضرب و تقسيم اعداد مخلوط
در ضرب و تقسيم اعداد مخلوط هم درست مثل جمع و تفريق، ميتوان به جاي آنها از كسرهاي متعارفشان استفاده كرد، قوانين اعداد گويا را به كار برد و در صورت لزوم حاصل را دوباره به شكل اعداد مخلوط برگرداند.
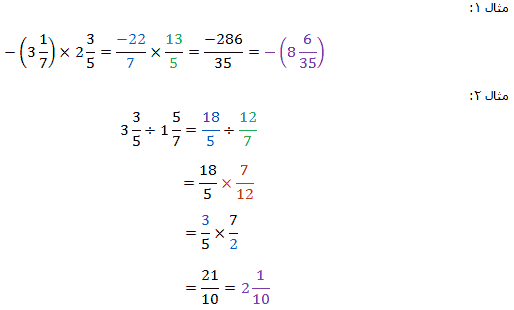
کاربرگ ضرب و تقسیم اعداد مخلوط (با کلیک روی این لینک، یک فایل word دانلود خواهد شد که برای تمرین بیشتر باید آنرا تکمیل کرده و در صورت تمایل برای تصحیح به ایمیل ما ارسال نمایید.)
جمع و تفريق اعداد مخلوط

به صورت كسر سوم نگاه كنيد. بله حالا علت كاري را كه براي تبديل عدد مخلوط به كسر متعارف آن انجام ميشود را بهتر ميفهميم.
در جمع و تفريق اعداد مخلوط ميتوان به جاي آنها از كسرهاي متعارفشان استفاده كرد و در آخر حاصل را دوباره به شكل اعداد مخلوط برگرداند.
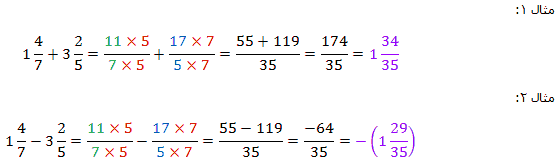
کاربرگ جمع و تفریق اعداد مخلوط (با کلیک روی این لینک، یک فایل word دانلود خواهد شد که برای تمرین بیشتر باید آنرا تکمیل کرده و در صورت تمایل برای تصحیح به ایمیل ما ارسال نمایید.)
تقسيم اعداد گويا
اين قسمت كمي سخت است ولي ما از عهدهاش برميآييم. درسته؟
خوب بگذار از اين يكي شروع كنيم:
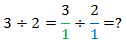
يعني 3 واحد كامل كه به 2 تقسيم شده باشند:

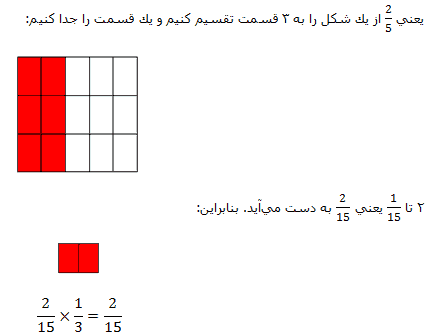
اوه! كم كم متوجه ميشويم كه به جاي تقسيم داريم از يك ضرب استفاده ميكنيم. اما علاوه بر علامت تقسيم، به جاي عدد دوم معكوس آن نوشته ميشود.
پس داريم يك قاعده جادويي براي تقسيم دو عدد گويا كشف ميكنيم. يعني ميتوان هر تقسيم را به ضرب عدد اول در معكوس عدد دوم تبديل كرد و ديگر از قوانين ضرب اعداد گويا استفاده كرد.
ديديد ما موفق شديم!
راستي گاهي تقسيم دو عدد گويا را به اين صورت هم نمايش ميدهند كه ظاهر ترسناكي هم پيدا ميكند و مخصوص ترساندن بچههاي ترسوست. اما با كشفي كه ما كرديم ديگر هيچ كسي نخواهد ترسيد:
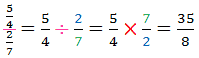
و اين يكي:
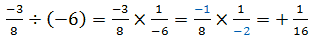
کاربرگ تقسیم اعداد گویا(تمرین و خودآزمایی)
آزمون تقسیم اعداد گویا (روی این لینک کلیک کنید و در صفحه بعد روی Create Test و سپس روی start کلیک کنید و جواب عباراتی که نشان داده میشود را به دست آورده و مقابل آن بنویسید)
